Objectif
Le tuto est pour objectif de discrétiser et implémenter sur Arduino une approximation de la dérivée seconde d’un fonction en utilisant la méthode des différences finies (DF).
Approximation de la dérivée seconde d’une fonction
Ci-dessous la formule mathématique de l’approximation de la dérivée secondes en utilisant la méthode des DF. Le paramètre h indique la période d’échantillonnage inverse de la fréquence d’échantillonnage de notre signal.
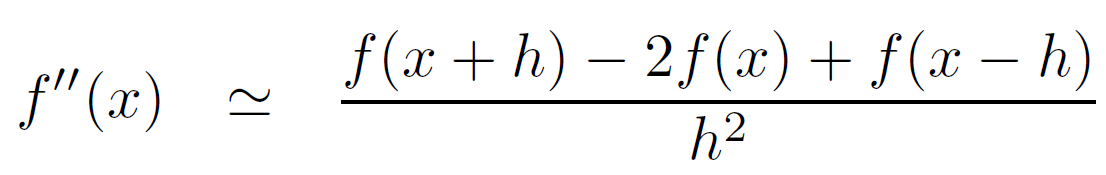
D’après la formule, l’approximation de la dérivée seconde est proportionnelle à f(n-1), f(n) et f(n+1) et inversement proportionnelle à h². On peut réécrire la formule sous forme du produit de convolution entre le filtre [1 -2 1 ] et le vecteur [f(n+1) f(n) f(n-1)]’. On verra dans la suite de la suite comment approximer la dérivée nième d’une fonction et comment calculer les coefficients du filtre.
L’erreur absolue de la méthode est proportionnelle à h²/12. Elle est environ deux fois plus petite par rapport à l’approximation de la dérivée première en utilisant l’approximation centrée (voir le tuto 4).
Comment implémenter la dérivée seconde ?
Principe
Le concept est semblable à celui de la dérivée premier (voir l’article précédent). L’approximation nécessite trois échantillons f(n+1), f(n) et f(n-1) symétriques par rapport à f(n). Par conséquent, durant l’implémentation on va utiliser un tableau de trois élément pour stocker les échantillons f(n), f(n-1) et f(n+1).
Attention, l’ordre est primordial durant le calcul de la dérivée !
Démarche d’implémentation
On déclare un tableau Tab[3] de trois élément ordonnés de la façon suivante [x(n) x(n-1) x(n-2)]. Pour chaque itération de la boucle on va effectuer les opérations suivantes :
- Acquisition de nouveau échantillon x(n+1)
- Décaler les éléments du tableaux Tab:
Tab[2] <= Tab[1]
Tab[1] <= Tab[0]
- Incrustation du nouvel échantillon dans le tableau
Tab[0] <= x(n+1)
- Calcul de l’approximations de la dérivée seconde :
x2_n=(Tab[0]- 2*Tab[1] + Tab[2])/T
Implémentation des approximations
La fonction diff2( ) sera utilisé pour le calcul de la dérivée seconde. Ci-dessous la déclaration et la définition de la fonction.
La fonction prend en entrée deux paramètres : le nouvel échantillon x(n+1) et la période d’échantillonnage en milliseconde. Puis, elle renvoie la valeur de l’approximation. La fonction renvoie un résultat par itération de la boucle. Ci-dessous la définition de la fonction diff2 ( ).
Le mot static permet de préserver les échantillons du tableau x[ ] entre les appels de la fonction. Sans utilisation du mot static, les échantillons d’avant seront perdus.
Test du programme
Pour tester les approximations on a besoin de générer une fonction f(n), puis on calcul sa dérivée en utilisant les trois approches. L’astuce consiste à générer une fonction triangulaire sous forme d’un compteur qui monte de 0 à une valeur maximale, puis décroit de la même façon à zéro. Du coup on obtient une fonction f(n)=n croissante et décroissante. Le résultat de la dérivée doit être sous forme d’un signal rectangulaire (voir la vidéo pour plus des détails). Ci-dessous un extrait du code dédié à la génération d’un signal triangulaire.

