
Domaines d’applications
- Filtrage actif et passif
- Capteurs passifs ( ou actifs)
- Réduction des harmoniques
- Limitation du courant au démarrage (condensateur moteur)
- Mise en forme des signaux
- Temporisateurs
- Oscillateurs harmoniques
- Doubleur de tension
- Mémoires logiques
- Amplificateurs et filtres RF
- Utilisé partout en électronique
Qu-est ce qu’un condensateur ?
Les condensateurs permettent d’emmagasiner des charges électriques et donc de l’énergie électrique. Un condensateur est constitué de deux conducteurs placés à proximité l’un de l’autre, mais sans qu’il y ait contact entre eux. La figure X.1.a offre un exemple typique de condensateur consistant en une paire de plaques parallèles, d’aire A, situées à une faible distance d l’une de l’autre ; on les appelle les armatures du condensateur.
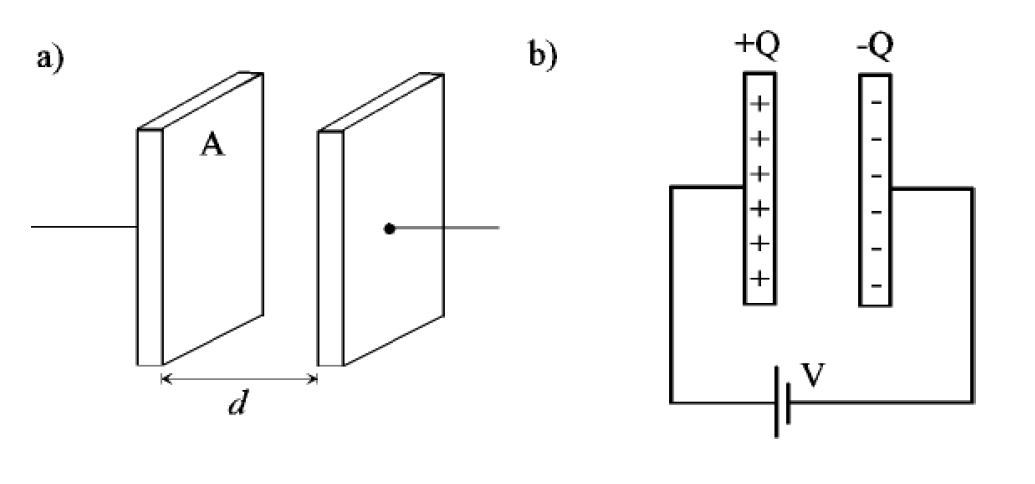
Lorsqu’on applique une tension aux armatures d’un condensateur, par exemple à l’aide d’une pile, il s’électrise rapidement : l’armature reliée à la borne positive de la pile porte une charge +Q tandis que celle reliée à la borne négative de la pile porte une charge égale et opposée –Q. Ceci résulte de ce que des électrons provenant de l’électrode négative de la pile s’écoulent vers l’armature du condensateur à laquelle elle est reliée par un fil conducteur. Cette armature portant une charge –Q repousse les électrons de l’armature opposée par induction et ceux-ci rejoignent l’électrode positive de la pile qui les attire ; cette armature porte une charge +Q. Dans les schémas de circuits électriques, on représente les condensateurs par :—| |—.
La capacité d’un condensateur
On constate que pour un condensateur donné, la charge Q portée par ses armatures est proportionnelle à la différence de potentiel V qu’on y applique. La constante de proportionnalité de cette relation, C, est appelée capacité du condensateur :
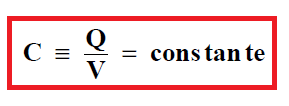
L’unité du système SI pour la capacité est le farad (F) ; c’est la capacité d’un condensateur qui porte 1 coulomb sur ses armatures lorsqu’on lui applique une différence de potentiel d’un volt : 1 F ≡ 1 C / V. La capacité est une constante propre à chaque condensateur. Sa valeur dépend de la taille, de la forme, de la position relative des deux conducteurs qui le constituent, ainsi que de la substance isolante, appelée diélectrique, qui sépare éventuellement les deux armatures.
Remarque :
- Contrairement à ce que peut suggérer à première vue la relation ci-dessus, la capacité ne dépend ni de V, ni de Q : si l’une de ces quantités est doublée, l’autre l’est aussi de manière à garder le rapport et donc C constant.
- On peut déterminer la capacité d’un condensateur de façon expérimentale à partir de la relation ci-dessus, en mesurant la charge Q de l’une de ses armatures, après l’avoir soumis à une différence de potentiel connue V.
- Dans le cas de condensateurs ayant une forme géométrique simple, la capacité peut se calculer. Prenons par exemple le condensateur à armatures parallèles, séparées par du vide, représenté sur la figure ci-dessous.
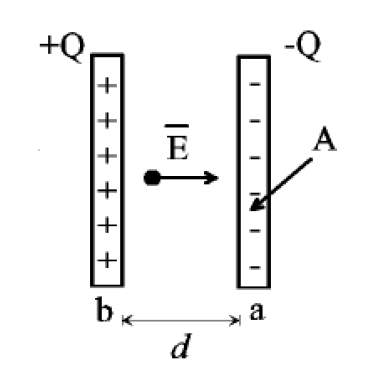
Ses plaques d’aire A portent une charge +/- Q et sont séparées par une distance d qu’on suppose faible par rapport aux dimensions des armatures. Dès lors on peut faire l’approximation que les plaques sont infinies et le champ électrique qui règne entre celles-ci vaut [latex] \sigma/\epsilon_0[/latex] et est dirigé de la plaque positive vers la plaque négative Dès lors :
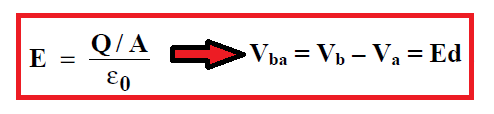
Ce qui conduit et donne pour un condensateur à armatures parallèles séparées par du vide:
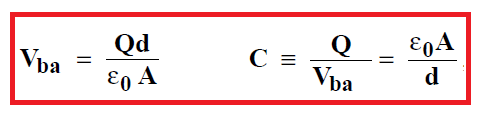
On voit qu’effectivement, la capacité ne dépend ni de Q, ni de V, seulement de l’aire des plaques et de la distance entre elles, ainsi que du milieu qui sépare les deux plaques. En effet, nous verrons à la section suivante que lorsqu’on place un isolant entre les deux plaques, il faut remplacer [latex] \epsilon_0[/latex], la permittivité du vide, par [latex] \epsilon[/latex], la permitivié de l’isolant.
Rôle des diélectriques dans un condensateur
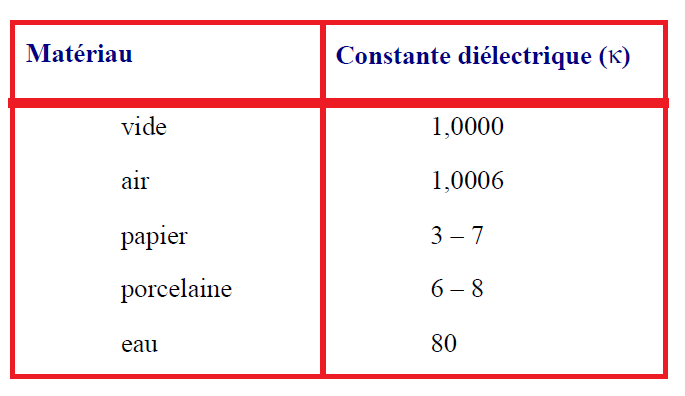
La plupart des condensateurs renferment une feuille de matériau isolant (papier, plastique, etc.), appelé diélectrique, qui sépare leurs armatures, et cela pour différentes raisons. D’abord les diélectriques empêchent plus efficacement que l’air ou le vide, les charges de passer d’une armature à l’autre, ce qui aurait pour effet de décharger le condensateur. La présence d’un diélectrique permet d’appliquer de plus hautes tensions avant de provoquer la décharge du condensateur. Elle permet aussi de rapprocher les armatures sans risquer qu’elles se touchent, ce qui accroît la capacité. Enfin, on a constaté expérimentalement que lorsqu’un diélectrique remplit l’espace compris entre les armatures d’un condensateur, sa capacité augmente d’un facteur (k> 1), appelé constante diélectrique : C = k Co. Où Co désigne la capacité du condensateur lorsqu’il y a le vide entre ses armatures et C celle du même condensateur avec un diélectrique de constante k entre ses armatures. La valeur de k varie avec la nature du diélectrique et se mesure expérimentalement. Le résultat de ces mesures se trouve consigné dans des tables. Quelques valeurs sont données à titre d’exemple dans le tableau.
Dans le cas d’un condensateur à armatures parallèles, séparées par un diélectrique de constante diélectrique k, on obtient en combinant les relations précédentes pour un condensateur à armatures parallèles:
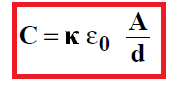
On pose [latex] \epsilon=k\epsilon_0[/latex]. On appelle la permittivité du diélectrique. L’augmentation de la capacité d’un condensateur dont les armatures sont séparées par un diélectrique provient de la polarisation de ce dernier. Certains électrons atomiques, attirés par la plaque positive, se déplacent légèrement vers celle-ci de telle sorte que bien que le diélectrique soit globalement neutre, la position moyenne des charges négatives est légèrement déplacée par rapport à la position des charges positives, attirées elles par la plaque négative.
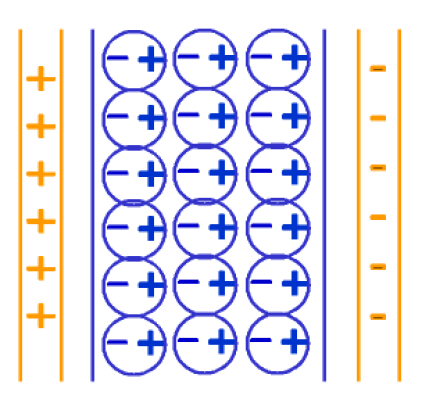
Les molécules polarisées donnent lieu à un champ électrique dirigé de leur charge + vers leur charge -, de sens opposé à celui créé par les plaques chargées. Par conséquent le champ électrique entre les plaques diminue ainsi que la différence de potentiel entre les plaques si celles-ci ne sont pas connectées et que les charges ne peuvent pas s’échapper :
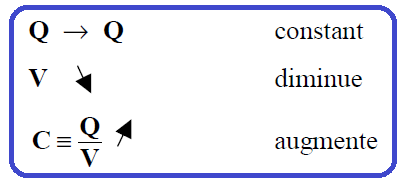
Si les plaques sont connectées à une pile lorsqu’on introduit le diélectrique, la pile maintient V constant et c’est la charge portée par les plaques qui va augmenter.
Les condensateurs en série et en parallèle
Tout comme les résistances, les condensateurs peuvent être associés en série ou en parallèle (voir figures a et b). Lorsque les condensateurs sont branchés en série, ils portent nécessairement tous la même charge Q. En effet, si une charge +Q s’écoule de l’électrode positive de la pile sur l’armature gauche du premier condensateur, il apparaît, par induction, une charge –Q sur l’autre armature. Comme cette dernière est connectée à l’armature gauche du deuxième condensateur par un fil conducteur, il apparaîtra une charge +Q sur cette dernière. En effet les deux armatures connectées par un fil conducteur forment un conducteur unique, isolé du monde extérieur ; la charge totale doit donc y rester nulle. De proche en proche, les condensateurs placés en série se chargent donc de la même charge : +Q, pour l’armature gauche, -Q, pour l’armature droite. La différence de potentiel aux bornes de chacun des condensateurs vaut par conséquent :
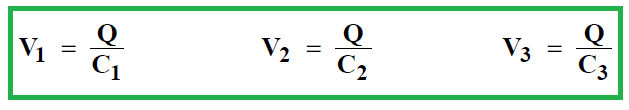
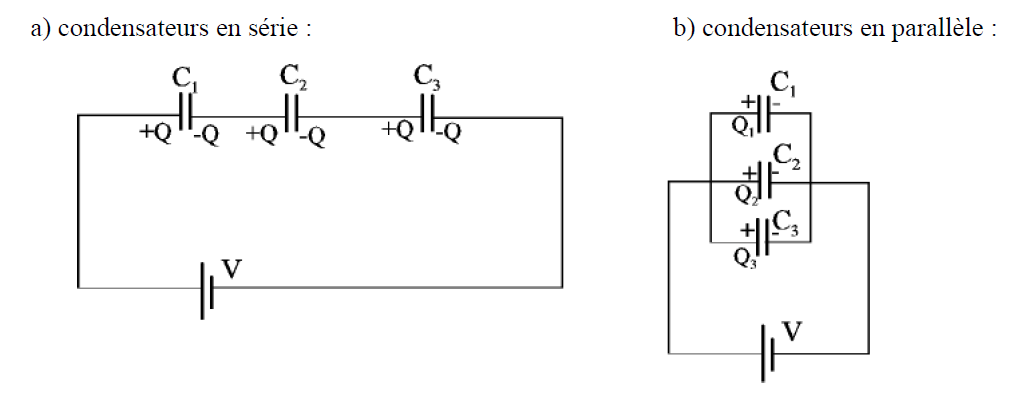
La loi des mailles donne : V = V1 + V2 + V3. Si C est la capacité de l’ensemble formé par les trois condensateurs en série, nous avons donc :
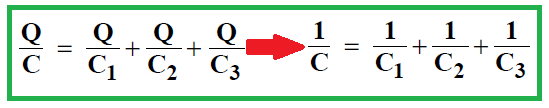
Lorsque les condensateurs sont branchés en parallèle, la différence de potentiel à leurs armatures est la même : V1 = V2 = V3 = V. D’autre part, la charge totale Q qui s’est écoulée des électrodes de la pile vaut : Q = Q1 + Q2 + Q3, où Q1, Q2 et Q3 sont les charges portées par les armatures de chacun des trois condensateurs, ceci en raison de la conservation de la charge. Si C est la capacité de l’ensemble formé par les trois condensateurs en parallèle : CV = C1 V + C2 V + C3 V. En divisant les deux membres par V, il vient :
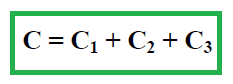
L’énergie électrique emmagasinée par un condensateur
Un condensateur emmagasine une quantité d’énergie électrique égale au travail accompli pour le charger, par exemple à l’aide d’une pile. Supposons qu’à un instant donné, la charge déjà accumulée sur les armatures soit q. Dès lors, la différence de potentiel entre les armatures vaut q / C. Le travail nécessaire pour faire passer une charge infinitésimale dq de l’armature négative à l’armature positive, via la pile est : dW = (q / C) dq. Le travail total W, pour charger un condensateur non chargé avec une charge Q s’obtient en intégrant :
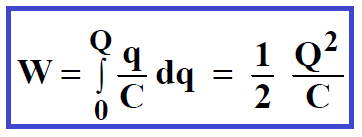
Ce travail est emmagasiné sous forme d’énergie potentielle électrique, UE. Comme on a la relation Q = CV, où V est la différence de potentiel de la pile, l’énergie potentielle électrique peut s’écrire sous trois formes différentes :
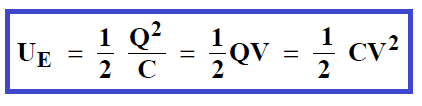
Comment tester un condensateur ?
Les circuits RC
Les circuits dont nous avons parlé jusqu’à présent, alimentés par une pile, étaient des circuits parcourus par des courants continus. Lorsqu’on inclut un condensateur dans un circuit alimenté par une pile, le courant varie en fonction du temps pendant la charge et la décharge du condensateur, ensuite il devient nul dans les branches où se trouve un condensateur.
La charge du condensateur
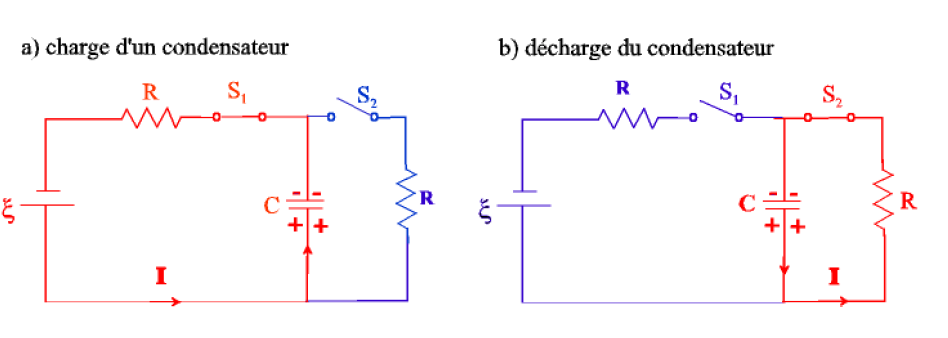
Supposons que le condensateur soit initialement non chargé (Q0 = 0) et que les deux interrupteurs, S1 et S2 soient ouverts. Aucun courant ne circule dans aucune branche du circuit car il n’y a pas de maille fermée : le condensateur reste non chargé. Supposons qu’à l’instant t = 0, on ferme l’interrupteur S1, on se trouve en présence d’un circuit à une maille, comportant une différence de potentiel e, fournie par la pile. Par conséquent un courant I s’établit, s’écoulant de la borne positive de la pile vers la borne négative. Ce courant amène des électrons sur l’armature supérieure du condensateur qui prend une charge –Q tandis que l’armature inférieure prend une charge +Q, des électrons rejoignant la borne positive de la pile. La loi des mailles nous permet d’écrire qu’à tout instant :
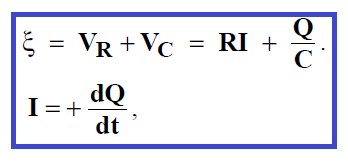
Ce qui donne l’équation différentielle suivante:
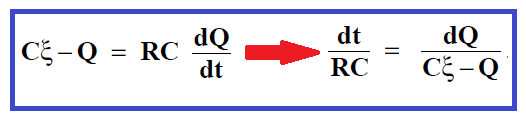
En intégrant les deux membres, où k est une constante d’intégration fixée par les conditions initiales. En t = 0, Q = 0 ; dès lors, nous avons :
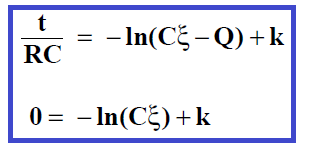
On trouve:
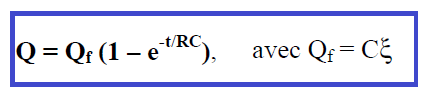
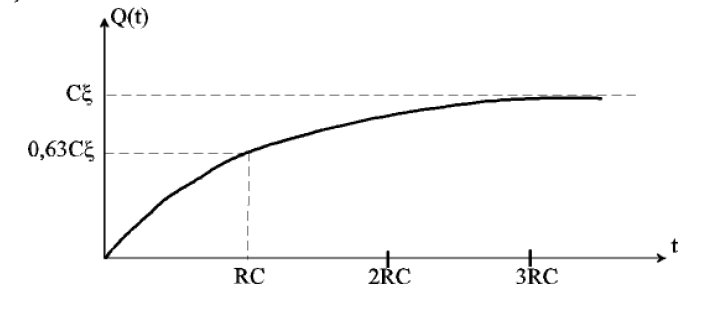
Elle représente le temps requis pour que le condensateur atteigne une charge Q = Qf (1 – e-1) = 0,63 Qf, ou 63% de la charge finale Qf. Ainsi, le produit RC constitue une mesure de la vitesse à laquelle le condensateur accumule de la charge. Il semble que le condensateur n’atteigne jamais la charge maximale Qf : il atteint 86% de cette valeur en 2 RC, 95% en 3 RC, 98% en 4 RC, etc. Par exemple si R = 30 ke et C = 0,20 μF, la constante de temps vaut (3,0 × 104 Ù) × (2,0 × 10-7 F) = 6,0× 10-3 s. Le condensateur atteint 98% de sa charge maximale en moins de 1/40 de seconde.
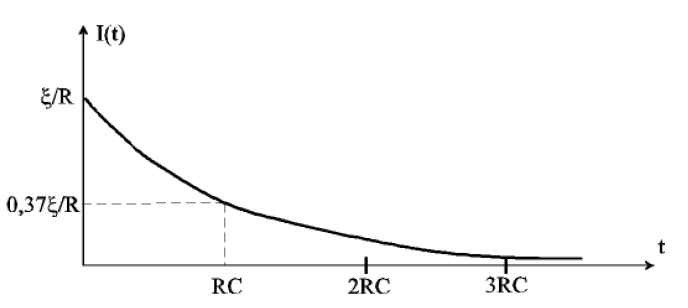
Pour obtenir l’intensité du courant qui charge le condensateur, il suffit de combiner les relations précédentes. Ainsi, à l’instant t = 0, le courant est maximum et vaut e/R. Il décroît ensuite de manière exponentielle, avec la constante de temps RC, de sorte qu’il ne vaut plus que 1/e = 0,37 de sa valeur initiale au bout d’un temps RC. Il tend vers zéro lorsque le temps tend vers l’infini.
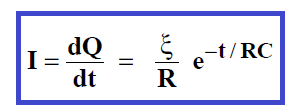
La décharge du condensateur
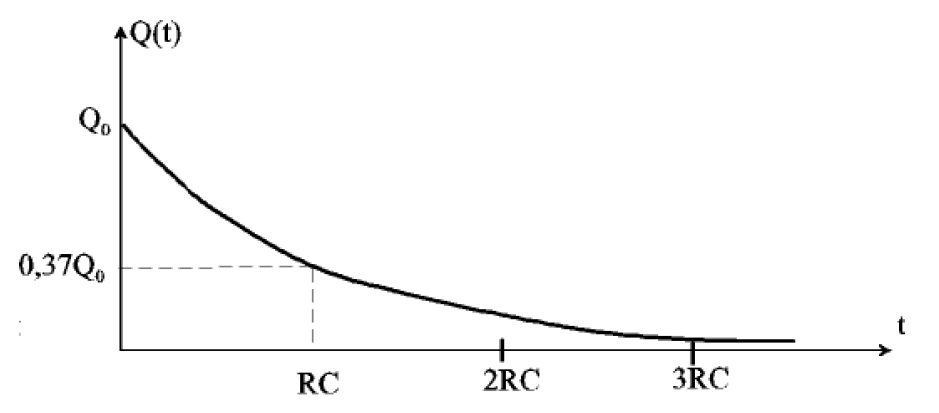
Supposons que le condensateur du circuit de la figure X.5 ait eu le temps de se charger complètement et porte donc la charge initiale Q0 =Ce. Le courant est devenu pratiquement nul. On ouvre l’interrupteur S1 et à l’instant t= 0, on ferme l’interrupteur S2. On se trouve en présence d’un circuit à une maille comportant une différence de potentiel Vc=Q/C fournie par le condensateur. Par conséquent, un courant I s’établit, s’écoulant de l’armature chargée positivement du condensateur, vers celle chargée négativement, en sens inverse du courant de charge. Ce courant amène des électrons de la plaque négative à la plaque positive, au travers de la résistance R. Tout calcul fait, avec Q0 la charge pour t=0:
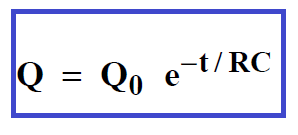
Exemples
-
Condensateur moteur: Condensateur Démarrage Moteur, 6μF, ±5%, 470V ac
-
Condensateur de démarrage
-
Condensateur variable: 5.0 → 60pF, 250V CC
-
Condensateur volet roulant: Exemple 3.5μF, ±5%, 450V AC
-
Condensateur électrolytique: Exemple aluminium 470μF, 25V cc, série RS, Traversant, +105°C
-
Condensateur polyester: Exemple 10nF, ±10%, 220 V c.a., 400 V c.c., Traversant, pas de 10mm, 368, MKT368
-
Condensateur ventilateur: Exemple polypropylène PP, 14μF, pas de 20.6mm

